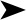How to add two 3 x 3 matrices on a GDC (graphical display calculator). This explanation uses the TI-82/83/84 range of calculators.The calculator has memory slots set aside for matrices: [A], [B], ..., [J].
1. Press the MATRIX key. This brings you to a menu with a list of all the matrices.
2. Use the right-arrow twice to move over to EDIT so that you can create a matrix.
3. Type a 1 (or ENTER) for matrix [A].
4. Press 3 ENTER 3 ENTER to indicate a 3x3 matrix.
5. Now choose values of the elements of the matrix until you've filled the matrix.
6. Return to the main screen by pressing 2ND MODE.
7. Repeat the last 4 steps to create matrix B.
8. Press MATRIX then ENTER
9. Press the + button
10. Press MATRIX then 2 then ENTER
A display of the sum A + B will be shown. Use the cursor keys to move about the matrix to see all the entries.
Software/Applets used on this page
This question appears in the following syllabi:
| Syllabus | Module | Section | Topic | Exam Year |
|---|---|---|---|---|
| AQA A-Level (UK - Pre-2017) | FP4 | Matrix algebra | 3x3 matrices | - |
| AQA A2 Further Maths 2017 | Pure Maths | Further Matrices | 3x3 Matrices | - |
| AQA AS/A2 Further Maths 2017 | Pure Maths | Further Matrices | 3x3 Matrices | - |
| CBSE XII (India) | Algebra | Determinants | Determinant of a square matrix (up to 3 x 3) | - |
| CCEA A-Level (NI) | FP1 | Matrix algebra | 3x3 matrices | - |
| Edexcel A-Level (UK - Pre-2017) | FP3 | Matrix algebra | 3x3 matrices | - |
| Edexcel AS Further Maths 2017 | Core Pure Maths | Matrices | 3x3 Matrices | - |
| Edexcel AS/A2 Further Maths 2017 | Core Pure Maths | Matrices | 3x3 Matrices | - |
| Methods (UK) | M5 | Matrix algebra | 3x3 matrices | - |
| OCR A-Level (UK - Pre-2017) | FP1 | Matrix algebra | 3x3 matrices | - |
| OCR AS Further Maths 2017 | Pure Core | Determinants, Inverses and Equations | 3x3 Matrices | - |
| OCR MEI A2 Further Maths 2017 | Core Pure B | Matrices and Transformations | 3x3 Matrices | - |
| OCR-MEI A-Level (UK - Pre-2017) | FP1 | Matrix algebra | 3x3 matrices | - |
| Pre-Calculus (US) | E2 | Matrix algebra | 3x3 matrices | - |
| Scottish Advanced Highers | M3 | Matrix algebra | 3x3 matrices | - |
| Scottish (Highers + Advanced) | AM3 | Matrix algebra | 3x3 matrices | - |
| Universal (all site questions) | M | Matrix algebra | 3x3 matrices | - |
| WJEC A-Level (Wales) | FP1 | Matrix algebra | 3x3 matrices | - |