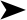The statement e^{i \theta} = \cos \theta + i \sin \theta \quad is known as Euler's relation (and as Euler's formula) and is considered the first bridge between the fields of algebra and geometry, as it relates the exponential function to the trigonometric sine and cosine functions.
If you substitute \theta = \pi the relation simplifies to e^{i\pi} =-1 \quad, known as Euler's identity.
If you substitute \theta = \pi the relation simplifies to e^{i\pi} =-1 \quad, known as Euler's identity.
Summary/Background
 Leonhard Euler (15 April 1707 – 18 September 1783) was a Swiss mathematician who made enormous contributions to a wide range of mathematics and physics including analytic geometry, trigonometry, geometry, calculus and number theory. Euler's work in mathematics is so vast that an article of this nature cannot but give a very superficial account of it. He was the most prolific writer of mathematics of all time. He made large bounds forward in the study of modern analytic geometry and trigonometry where he was the first to consider sin, cos etc. as functions rather than as chords as Ptolemy had done.
Leonhard Euler (15 April 1707 – 18 September 1783) was a Swiss mathematician who made enormous contributions to a wide range of mathematics and physics including analytic geometry, trigonometry, geometry, calculus and number theory. Euler's work in mathematics is so vast that an article of this nature cannot but give a very superficial account of it. He was the most prolific writer of mathematics of all time. He made large bounds forward in the study of modern analytic geometry and trigonometry where he was the first to consider sin, cos etc. as functions rather than as chords as Ptolemy had done.
He made decisive and formative contributions to geometry, calculus and number theory. He integrated Leibniz's differential calculus and Newton's method of fluxions into mathematical analysis. He introduced beta and gamma functions, and integrating factors for differential equations. He studied continuum mechanics, lunar theory with Clairaut, the three body problem, elasticity, acoustics, the wave theory of light, hydraulics, and music. He laid the foundation of analytical mechanics, especially in his Theory of the Motions of Rigid Bodies (1765).
The number e = 2.718281828459 is Euler's number, the base of the natural logarithm. Euler's identity, e^{i\pi} + 1 = 0 is also sometimes called Euler's equation.
Software/Applets used on this page
This question appears in the following syllabi:
| Syllabus | Module | Section | Topic | Exam Year |
|---|---|---|---|---|
| AQA A-Level (UK - Pre-2017) | FP2 | Complex Numbers | Euler relation | - |
| AQA A2 Further Maths 2017 | Pure Maths | Further Complex Numbers | Euler Relation | - |
| AQA AS/A2 Further Maths 2017 | Pure Maths | Further Complex Numbers | Euler Relation | - |
| CCEA A-Level (NI) | FP2 | Complex Numbers | Euler relation | - |
| CIE A-Level (UK) | P3 | Complex Numbers | Euler relation | - |
| Edexcel A-Level (UK - Pre-2017) | FP2 | Complex Numbers | Euler relation | - |
| Edexcel A2 Further Maths 2017 | Core Pure Maths | Complex Numbers | Euler Relation | - |
| Edexcel AS/A2 Further Maths 2017 | Core Pure Maths | Complex Numbers | Euler Relation | - |
| I.B. Higher Level | 1 | Complex Numbers | Euler relation | - |
| Methods (UK) | M3 | Complex Numbers | Euler relation | - |
| OCR A-Level (UK - Pre-2017) | FP3 | Complex Numbers | Euler relation | - |
| OCR A2 Further Maths 2017 | Pure Core | Further Complex Numbers | Euler Relation | - |
| OCR MEI A2 Further Maths 2017 | Core Pure B | Complex Numbers | Euler Relation | - |
| OCR-MEI A-Level (UK - Pre-2017) | FP2 | Complex Numbers | Euler relation | - |
| Scottish Advanced Highers | M2 | Complex Numbers | Euler relation | - |
| Scottish (Highers + Advanced) | AM2 | Complex Numbers | Euler relation | - |
| Universal (all site questions) | C | Complex Numbers | Euler relation | - |
| WJEC A-Level (Wales) | FP2 | Complex Numbers | Euler relation | - |